![]()
CHAPTER 3 - VEGETATION STRUCTURE AS AN INDICATOR FOR LAND-COVER DYNAMICS ASSESSMENT IN THE AMAZON
3.3. Data analysis
The steps carried out for data analysis are illustrated in Figure 13. The following sections describe the main procedures implemented. Special attention was given to the definition of vegetation structural variables and the analysis of spectral data in order to achieve a better knowledge about the regrowth stages present in the study area.
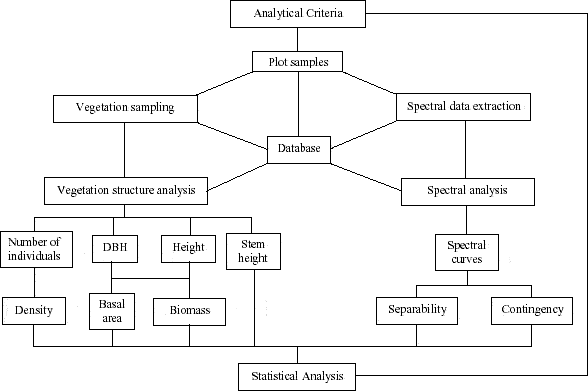
Figure 13 - Integration of vegetation structure and spectral data analysis for Machadinho d’Oeste and Vale do Anari.
3.3.1. Descriptive comparisons through photos and vegetation profiles
A first picture about the variation in vegetation structure from the early stages after abandonment up to forest is given by visual characteristics. After some training it becomes easier to decide between distinct classes mainly if a small number of possible choices is assigned (i.e., SS1, SS2, SS3, and forest). Of approximate character, the distinction of classes is not very evident in the beginning but becomes consistent after field experience. Following Daget and Godron (1982), the classification is appropriate when the observer hesitates in deciding between two and only two neighbor classes. This hesitation becomes acceptable after preliminary surveys and means that the classes are well adapted to the description of the actual heterogeneity within the plot sample.
Certainly, when making those decisions, an ecologist is intuitively using variables such as height, biovolume, ground cover, dominant and indicator species, among others. To help the analysis, an extensive photo collection was generated. Each photo received the survey number to allow further examination as a register about the ecological condition of each sampling site. On the other hand, several vegetation profiles were drawn to complete the graphic representation of vegetation structure.
3.3.2. Variables analyzed
Some specific variables were calculated based on collected field data with the purpose of characterizing vegetation stands in a quantitative basis. As the focus was on structure rather than species composition, all variables were calculated for size classes, mainly the dominant strata (i.e., trees and saplings). Literature review about the study of secondary succession in the tropics provided insights about the variables to use. Formulas and definitions were compiled from Mueller-Dombois and Ellenberg (1974), Greig-Smith (1983), Schreuder et al. (1993), and Kent and Coker (1994). In the equations given below, the following abbreviations are used: DBH = diameter at breast height; BA = basal area; H = height; Y = biomass.
The number of individuals of a size class in the stand is important to characterize vegetation. Density is determined by counting the number of individuals of each size class on each sample plot, and then estimating the average number of stems of each size class per unit area sampled.
Diameter at breast height is the most frequently measured variable in vegetation surveys and has multiple uses. Overbark diameter measurements at breast height (1.5 m from the ground) are quick, easy, inexpensive, relatively accurate, and usually correlated with other variables, such as basal area, volume or biomass. In the field, DBH was measured with diameter tape and averaged for the classes of interest (i.e., trees and saplings). It is expressed in centimeters.
Basal area is the horizontal (cross-sectional) area occupied by the trunk of a species or size class. It is expressed in square meters per hectare (m2/ha) and its formula is:
BA = (DBH/2)2 * p / area sampled
Total height is a straightforward parameter used for direct measurement purposes and also for the calculation of volume or biomass. It is expressed in meters. Once in a stand, the height of some trees was measured with a hand-held clinometer. The values obtained were used as controls for height estimation of other trees and saplings using a five-meter rod as a reference. The estimation was crosschecked between two or three observers to achieve consensus.
Biomass is the equivalent weight of an individual or group of individuals (e.g., trees and saplings). The method of calculation can be destructive (actually cutting and weighing what is being measured) or an estimation, based on allometric equations. It can be measured for aboveground biomass, belowground biomass, wood biomass, leaf biomass, and fruit biomass. In this research, the analysis was restricted to aboveground biomass through the use of two allometric equations for its estimation. Due to its application to forested areas in Rondônia, the equation given by Brown et al. (1995) was used for trees with DBH greater than 10cm, where:
Y = 0.0326 * (DBH)2 * H
For saplings (2.5 cm < dbh < 10 cm), the equation given by honzák et al. (1996) was used, where:
Y = exp[-3.068 + 0.957 ln (D2 * H)]
Caution should be taken when analyzing aboveground biomass estimations, as they are dependent on several variables such as hollowness, wood density for every species, bark, presence of palms, vines, and dead biomass (Fearnside 1992). The goal of these estimations was to have another parameter for comparison across the size classes (i.e., trees and saplings) and vegetation formations (i.e., SS1, SS2, SS3, and forest) within the study area.
Some ratios between variables were also calculated. Inspired by previous work (Tucker 1996, Tucker et al. 1998), the goal was to depict the contribution of each major group of plants (i.e., trees and saplings) in relation to values found for the entire vegetation formation or for the other group. Therefore, three ratios are presented in this chapter:
Density of saplings to density of trees
Percent tree contribution to total basal area
Percent sapling contribution to total basal area
3.3.3. Integration of spectral data
One of the main goals of fieldwork was to collect sufficient data to carry out the multi-temporal supervised classification of satellite images. For the purpose of image analysis, each plot sample became a 'training sample,' that is, an area of known identity that is used during supervised classification to identify areas of unknown identity (Mausel et al.1990). Each one of these areas was selected as an 'area of interest' (AOI) with specific spectral characteristics. GPS collected points and color composite printouts used in the field allowed the accurate positioning of each of these areas. The mean reflectance for the training samples was extracted for each TM band as well as the value for the Normalized Difference Vegetation Index (NDVI) (Lillesand and Kiefer 2000). The values were exported to the corresponding table in the database to allow their integration with vegetation structure data.
3.3.4. Statistical analysis
The first step to achieve a better understanding about a specific set of numeric data is to perform an exploratory data analysis (Burt and Barber 1996). There are several methods, techniques, and statistical packages to accomplish this task. The first approach focused on graphic methods of analysis. Quantitative methods were used to inform the discussion in terms of the scientific motivation for this chapter.
Graphs are tools for analysis and communication (Schmid 1983). They provide a different perception about data, summarizing observations based on some defined output. Cleveland and McGill (1985) have shown that graphical methods are successful if the decoding process is effective. Moreover, some methods are better than others in terms of graphical perception. To avoid problems during data interpretation, simple and effective graphical methods such as boxplots and scatterplots were used. A boxplot is a summary plot based on the median, quartiles, and extreme values. The box represents the interquartile range that contains 50% of the values. The whiskers are lines that extend from the box to the highest and lowest values, excluding outliers. A line across the box indicates the median. In the scatterplot, one numeric variable is plotted against another, representing graphically the distribution of both variables (Ott 1993).
After becoming familiar with data through graphic methods, a second type of analysis is done through numeric procedures. Statistics is generally defined as a methodology for collecting, presenting, and analyzing data. Multiple purposes are recognized for the use of statistics, including its capability to summarize data, validate theories, provide forecasts, evaluate trends, and select a particular sample of interest. Descriptive statistics is used to organize and summarize data. Inferential statistics combines descriptive statistics with probability theory, generalizing the results of a study of a few individuals to a larger group. The mean is the most commonly used measure of central tendency. It is the 'center of gravity' or the 'balancing point' of a set of observations. However, the mean does not account for the variability of data in the range of values. To determine how typical the measure of central tendency is in a distribution, it is necessary to analyze measures of dispersion. Standard deviation is the most commonly used measure of dispersion. Mean, standard deviation, minimum and maximum values were used for the study of structural vegetation variables.
Another numeric approach in exploratory data analysis is the study of statistical relations between two variables. Pearson's correlation coefficient and its significance levels were used to measure the strength of association between the variables under analysis.
Finally, analysis of variance (ANOVA) was used as a statistical technique designed to determine whether or not a particular classification of the data is meaningful. Data are decomposed to structure an F-test to test the hypothesis that the between-class variation is large relative to the within-class variation, which implies that there is a significant variation in the dependent variable between classes. The theoretical background about the procedures used and statistical significance of results obtained was based on literature about the topic (among others, Ott 1993, Shaw and Wheeler 1994, Gujarati 1999).